NumberMatch is a mobile puzzle game with the goal of matching pairs of identical digits or digits that sum to 10 until the grid is emptied.

The game starts with 35 random base 10 digits in a 9 column grid.

Each cell with a number can match to another number in a direct line (up, down, left, right, or any diagonal).

A game of Numbermatch begins with 35 digits displayed in a 9 column grid. This produces a final row with 8 digits and a blank cell (located at row 4, column 9).

There are numerous ways to scan the grid for initial matches. A simple approach would be to start in the first row and scan left to right. By scanning in this fashion, we only need to check for matches in these directions: right, down-left, down, down-right. For example, once we've checked the down match for two cells, when scanning the next row we do not need to check the up match.

For cells in the first column, this indicates three possible matching cells to check (down, down-right, right):

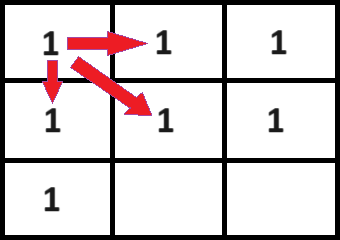
For columns 2 through 8, there are four possible matches (down, down-left, down-right, right):

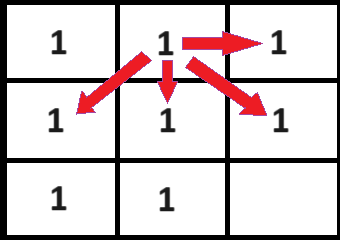
Column 9 is very similar to column 1 - there are three possible matches (down, down-left, wrap-around right):

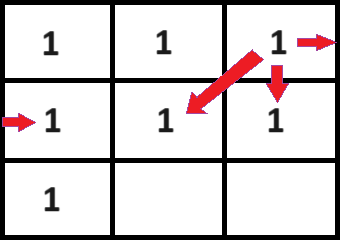
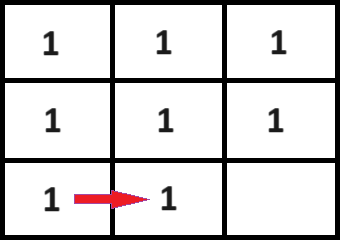
The possible matches for each row are the same until the second to last row. On that row, a non-complete final row will limit the down / down-left / down-right possibilities.

The final row will only need to check for matches to the right up to the final digit:

The total number of possible connections at the start is 107.

The expected number of matches on the first turn of Numbermatch can be calculated. Let's assume each cell is an independently random value between 1 and 9 inclusive. Two connected cells can match in the following ways:

1. The first cell is a 5 (1/9 prob) and the second cell is a 5 (1/9 prob). Odds of this occurring are 1/81.
2. The first cell is a non-5 number (8/9) and the second cell is the same number (1/9). Odds of this occurring are 8/81.
3. The first cell is a non-5 number (8/9) and the second cell is the complimentary number (1/9). Odds are 8/81.
4. Full odds of a match are 17/81.
5. 17/81 times 107 total connections to check equals 22.45679.

Unnecessary Math

If we wanted to build a variable column or starting digit count Numbermatch game, the number of initial possible matches would change based on this formula:

4rc - 2r - 7c + 4l + 2

With c representing the column count, r reprensenting the row count (ceiling of digits divided by c), and l equaling starting digits % c.

Starting boards in real games of Numbermatch have far fewer initial connection options than expected. As stated in the above section, for a randomly generated starting position we expect ~22 starting matches on average.

In testing actual starting boards through the Numbermatch app, the typical starting board only has ~3 to ~5 initial match options.

To help visualize how unlikely a typical real game would be, I generated 1 million random starting positions and calculated the initial match options:

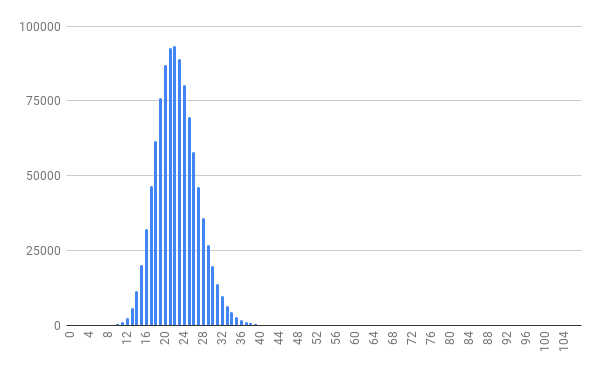
Here we can see a normalized distribution centered around the peak at 22 matches.

Since real world and random starting positions are vastly different, a method is needed to generate starting positions. This can be done by generating 35 random digits, checking the number of initial matches, breaking a random match (swapping one matching digit for a non-matching digit), and repeating until the match count is less than 5.

Side note: it is reasonable to assume this is done on purpose by the designers of the Numbermatch game. An initial board with a few matches requires some time to find the match. This may be more enjoyable to the player than having ~22 matches to choose from.

Below are some initial testing results for various strategies. The first set of numbers are for random starting positions. After the / character is a second set of numbers for starting positions that had 0 initial matches.

1. Random
• Select a random match to play at each step of the solve.
• Solve Success: 72% / 35%
• Avg Additions Remaining: 2.3 / 1.2
• Avg Matches Made: 27.6 / 58.8
2. Brute Force First Match
• Select the first match found (scan left to right, top to bottom).
• Solve Success: 81% / 61%
• Avg Additions Remaining: 2.5 / 1.4
• Avg Matches Made: 26.2 / 58.3
3. Match Direction
• Choose the first match based on match direction: right, down-left, down, down-right. "Right" was the most successful in testing.
• Solve Success: 84% / 63%
• Avg Additions Remaining: 2.4 / 1.3
• Avg Matches Made: 27.4 / 58.9
4. Target an Area of the Board
• Take matches from a specific part of the board if available.
• Not yet tested / implemented.
5. Prioritize Clearing Rows
• Select a match with a cell in a row with 3 or fewer remaining digits.
• If there a many rows with a low density of numbers, there could be a reduced number of diagonal match possibilities. Clearing rows should alleviate this problem.
• Not yet implemented / tested.
6. Prioritize Matching 5's
• The digit '5' can only match with itself, limiting match options. Clearing all 5's from the board should open paths for the other numbers.
• Not yet implemented / tested.
7. Target Digits with Fewest Cells Remaining
• Similar to the 5's strategy. Prioritize selecting matches for digits that appear the least on the board.
• This strategy should lower the complexity of the puzzle faster.
• Not yet implemented / tested.
8. 1-Depth Future Peek for Most Matches
• For each match of the current state, check the board state if that match is made, and count the matches available.
• This strategy helps keep the game active and may be beneficial in the endgame.
• If there are multiple matches that return the same future match count, the tied matches can be prioritized by another strategy.
• Solve Success: 96% / 86%
• Avg Additions Remaining: 2.8 / 2.0
• Avg Matches Made: 24.0 / 50.1
9. Backtrack when Board is Near End
• Utilize a full backtrack alogorithm when the board is near end.
• A full backtrack solution would be computational expensive. The starting position analysis shows an average of 22+ matches for a random starting position and an efficient solve makes ~30 matches.
• 22^30 possible paths is a gross over-estimate as the complexity decreases as matches are made. But this upperbound shows the initial state is very complex.
• Not yet tested / implemented.
10. Optimized Number Additions
• Perform a 1-depth peek if adding numbers will lead to a solution when the board is near end.
• Not yet implemented / tested.
11. Neural Network
• Use a neural network to attempt to solve.
• Not yet tested / implemented.

There are numerous possible configurations that can occur at the end of a game as remaining digits can be in many different cell positions.

However, all configurations will have a guaranteed connection path. The first remaining cell will connect to the second remaining cell to the right (either on the same row or as a wrap around to the next row). The second will match the same way to the third remaining digit and so on.

The board can be solved if a quasi-palindrome can be created - if the first digit matches the last digit, the second digit matches the second-to-last digit, and so on. The final set of moves would then be to take the middle match and then the rest of the matches propogating outwards.

Working backwards, the final match of a successful game will always be two matching cells and is not very interesting.

The second-to-last match state has 2 pairs of matching digits giving 6 total permutations. 4 of these are solvable (for example "1221" or "2211"). Only 2 permutations are not solvable ("1212" and "2121").

The third-to-last match state with 3 pairs of matching digits has 90 total permutations with 30 of them solvable. Solvable examples include "112233" and "321123". The puzzle could fail if it's "123123".

For four remaining unique digit matches, there are 2,520 possible configurations with 336 of them solvable. After that it's guaranteed to overflow into multiple rows, allowing more possible connections.

The equation to generalise the possible configurations is: (2p)! / 2^p where p is the number of pairs. For example, (2 * 4)! / 2^4 = 10! / 16 = 2,520.

And the equation to generalise the solvable combinations is: (2p)! / (p+1)! where p is again the number of pairs.

Run Ending Tests

Tests have not yet been run.

Please provide an input of 35 digits:

Submit

Choose number of starting positions to test (10k maximum):

Submit